3) Loi de Snell-Descartes
Comme nous l’avons écrit précédemment, ces lois résultent des travaux séparés de Descartes et de Snell datant d’il y a quatre siècles. Elles décrivent le comportement de la lumière à l’interface de deux milieux transparents et homogènes.
Tout d’abord, il faut savoir que ces lois découlent du principe de Fermat qui affirme que, dans un milieu homogène, les rayons lumineux empruntent le plus court chemin pour passer d’un point A à un point B et donc que cette propagation est rectiligne. Ce principe est donc à la base de la géométrie optique.
Lorsque la lumière rencontre un dioptre, une partie de cette dernière est réfractée dans le second milieu, tandis que l’autre partie de la lumière subit une réflexion : les rayons sont renvoyés dans leur milieu d’origine.
La loi de la réflexion stipule que les rayons incidents et réfléchis forment un angle dont la bissectrice est la normale au point d’incidence (voir schéma) : on a donc
i = i’
a) La réflexion

RAPPEL :
Le rayon lumineux est dit incident avant d’avoir rencontré la surface réfléchissante, il est dit réfléchi après.
Le point de rencontre du rayon incident et de la surface réfléchissante est appelé point d'incidence.
La droite orthogonale à la surface réfléchissante au point d'incidence est appelée normale.
L'angle θ1 est l’angle d’incidence et l’angle θ2 est appelé angle de réflexion.
On a θ2 = -θ1
Cela nous amènera au principe de réflexion totale qui est extrêmement important pour notre problématique puisqu’il nous faut savoir comment la fibre transmet la lumière sur de longues distances.

La loi de Snell-Descartes de la réfraction exprime le changement de direction d'un faisceau lumineux lors de la traversée d'une paroi séparant deux milieux différents. Chaque milieu est caractérisé par sa capacité à « ralentir » la lumière, modélisée par son indice de réfraction n qui s'exprime sous la forme : n= c/v où v est la vitesse de la lumière dans ce milieu et c la vitesse de la lumière dans le vide.
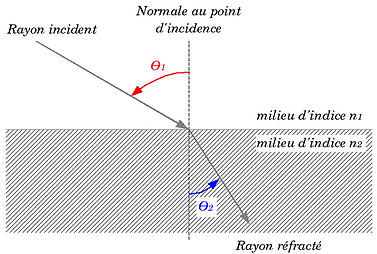
L'angle θ1 est l’angle d’incidence et l’angle θ2 est appelé angle de réfraction.
Soit n1 l'indice de réfraction du milieu dans lequel se propage le rayon incident et n2 celui du milieu dans lequel se propage le rayon réfracté.
La relation liant les indices de réfraction n1 et n2 de chacun des milieux et les angles incidents θ1 et réfracté θ2, appelée relation de Snell-Descartes s’écrit : n1 x sin(θ1) = n2 x sin(θ2).

b) Lois sur la réflexion
c) Lois sur la réfraction